site creation software

Research interests

Control of Partial Differential Equations
Control of Level Set Methods
Dynamic Mode Decomposition for Transitional flows
Wound Healing and tissue repair models
Level set methods in biological applications
Algorithms and scheduling for drones
Platform for managing drones
Employment of UAV for fighting wildfires 

Control of Level Set Methods

Level Set Methods (S. Osher, J. Sethian, J. of Computational Physics 1987) are a class of very popular methods to propagate interfaces. Our aim is to develop methodologies to control in time  fronts described by Level Set Methods. A project "C-LEVEL” was funded by US AFOSR, Air Force Office of Scientific Research. 

Development of algorithms and a scheduling dynamic system for managing drone swarms

M.A.R.S. is a patented platform developed by Inspire (Unige spin-off) that allows:

-  integrated logistic for drones deployment
– extended flight missions enabled by automatic battery replacement system
– fractionable payload management system
– collaborative drones flight in swarm configuration

Drone Swarms in Fire Suppression Activities

Recent huge technological development of Unmanned Aerial Vehicles (UAVs) can provide breakthrough means of fighting wildland fires. We have studied an innovative forest firefighting system based on the use of a swarm of hundreds of UAVs able to generate a continuous flow of ex-tinguishing liquid on the fire front, simulating rain effect. Automatic battery replacement and re-filling of the extinguishing liquid ensure the continuity of the action.

E. Ausonio, P. Bagnerini, M. Ghio, Drone Swarms in Fire Suppression Activities: a Conceptual Framework, Drones, vol.5, n.1, 2021 

Mobirise
Mobirise

Wound healing in Drosophila pupae

We study wound healing in collaboration with L. Neves de Almeida (Sorbonne Université) and with A. Jacinto, a biologist of the Lisboa University. We proposed continuous mathematical models where the wound is described by Level set methods. Currently, we are modeling a complex mechanism starting in the first minutes of wound healing.

Mobirise

Dynamic Mode Decomposition for fluid flows

The spatial and time behavior of fluid flows at different Reynolds numbers and stream turbulence intensity levels is analysed by combining dynamic mode decomposition and
moving horizon estimation in order to detect regime transitions. The norm of the residuals  in processing successive snapshots of the flow
velocity field shows a trend that is used to identify the change from stable and unstable
regimes. 

Selected Publications

- E. Ausonio, P. Bagnerini, M. Ghio, Drone Swarms in Fire Suppression Activities: a Conceptual Framework, Drones, vol.5, n.1, 2021.

- A. Alessandri, P. Bagnerini, M. Gaggero, L. Mantelli, Parameter Estimation of Fire Propagation Models Using Level Set Methods, Applied Mathematical Modelling, vol. 92, pp 731-747, 2021.

- M. Neviani, P. Bagnerini, O. Paladino, Gas Bubble Dynamics in Airlift Photo-bioreactors for Microalgae Cultivation by Level Set Methods, Fuel, vol. 292, 2021.

- A. Alessandri, F. Bedouhene, D. Bouhadjra, A. Zemouche, P. Bagnerini, Observer-based Control for a Class of Hybrid Linear and Nonlinear Systems, Discrete and Continuous Dynamical Systems - Series S, vol. 14, n.4, pp 1213-1231, 2021.

- A. Alessandri, P. Bagnerini, M. Gaggero, A. Rossi, State and Observer-based Feedback Control of Normal Flow Equations, Automatica, vol. 117, 2020.

- A. Alessandri,  P. Bagnerini, R. Cianci, S. Donnarumma, A. Taddeo, Stabilization of Diffusive Systems Using Backstepping and the Circle Criterion, International Journal of Heat and Mass Transfer, vol. 149, 2020.

- A. Alessandri, P. Bagnerini, R. Cianci, R. Revetria, Modeling and Estimation of Thermal Flows on Transport and Balance Equations, Advances in Mathematical Physics, 2020.

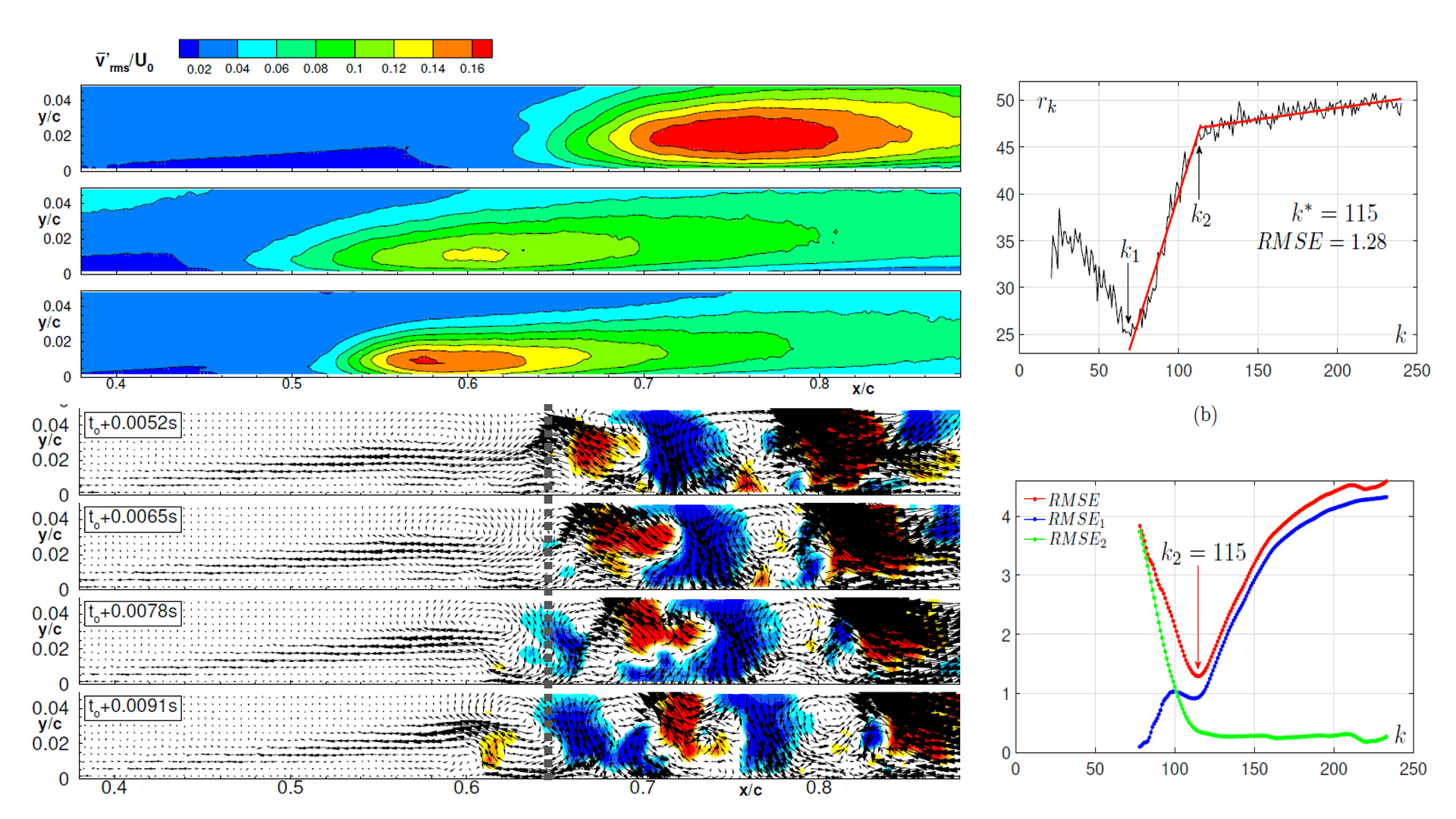
- A. Alessandri, P. Bagnerini, M. Gaggero, D. Lengani, D. Simoni, Dynamic Mode Decomposition for the Inspection of Three-Regime Separated Transitional Boundary Layers Using Least Squares Methods, Physics of Fluids, vol.31, n. 4, 2019.

- P. Bagnerini, G. Fabrini, B. D. Hughes, T. Lorenzi, L. Neves de Almeida, Evolution of Cancer Cell Populations Under Cytotoxic Therapy and Treatment Optimisation: Insight From a Phenotype-structured Model, ESAIM: Mathematical Modelling and Numerical Analysis (M2AN), vol.53, n.4, pp 1157-1190, 2019.

- A. Alessandri, P. Bagnerini, M. Gaggero, Optimal Control of Propagating Fronts by Using Level-Set Methods and Neural Approximations, IEEE Transactions on Neural Networks and Learning Systems, 30-3, pp 902-912, 2019.

- A. Alessandri, P. Bagnerini, M. Gaggero, D. Lengani, D. Simoni, Moving horizon trend identification based on switching models for data driven decomposition of fluid flows, in 57th IEEE Conf. on Decision and Control, Miami, Florida, USA, pp. 2138–2143, 2018.

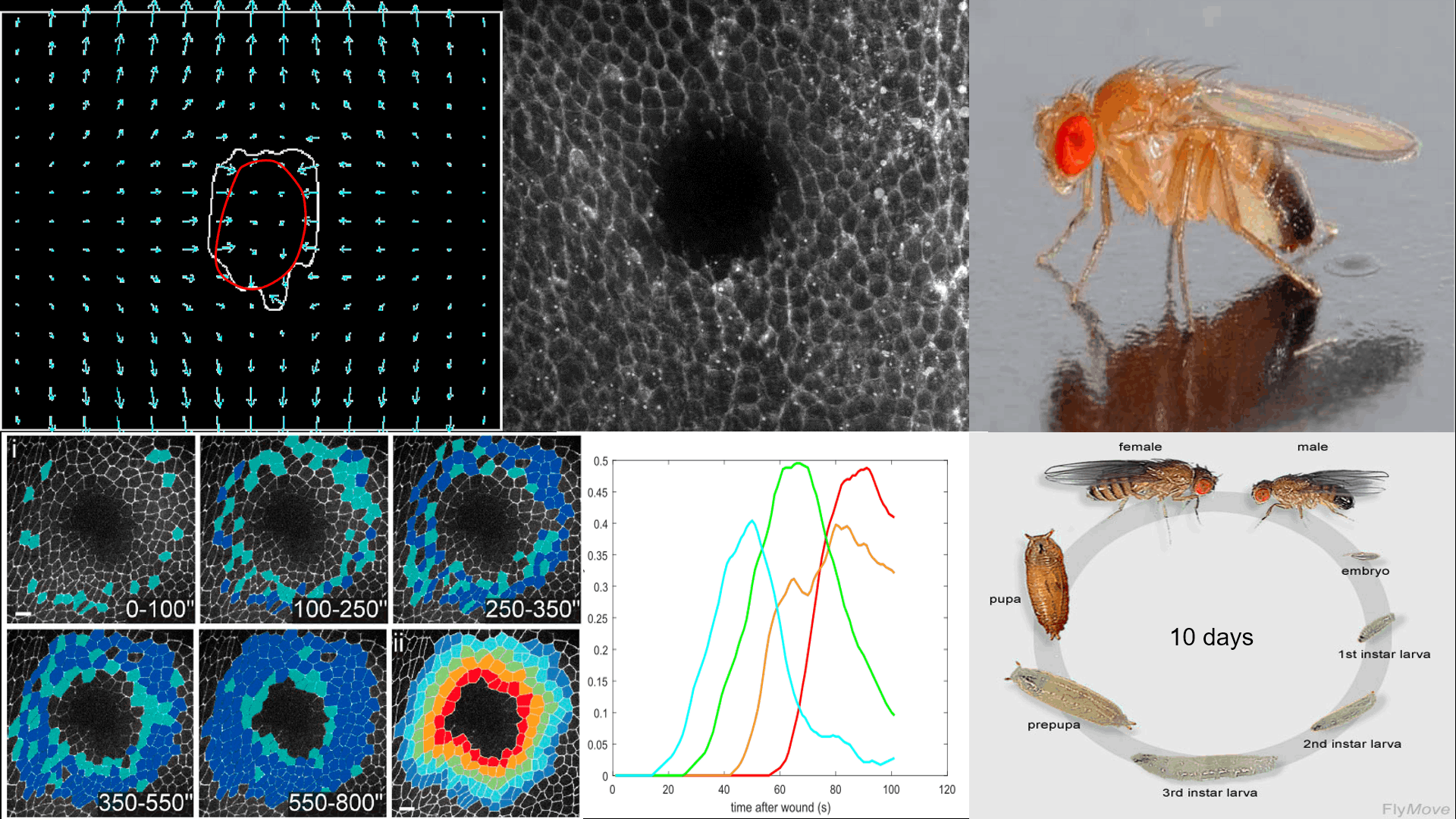
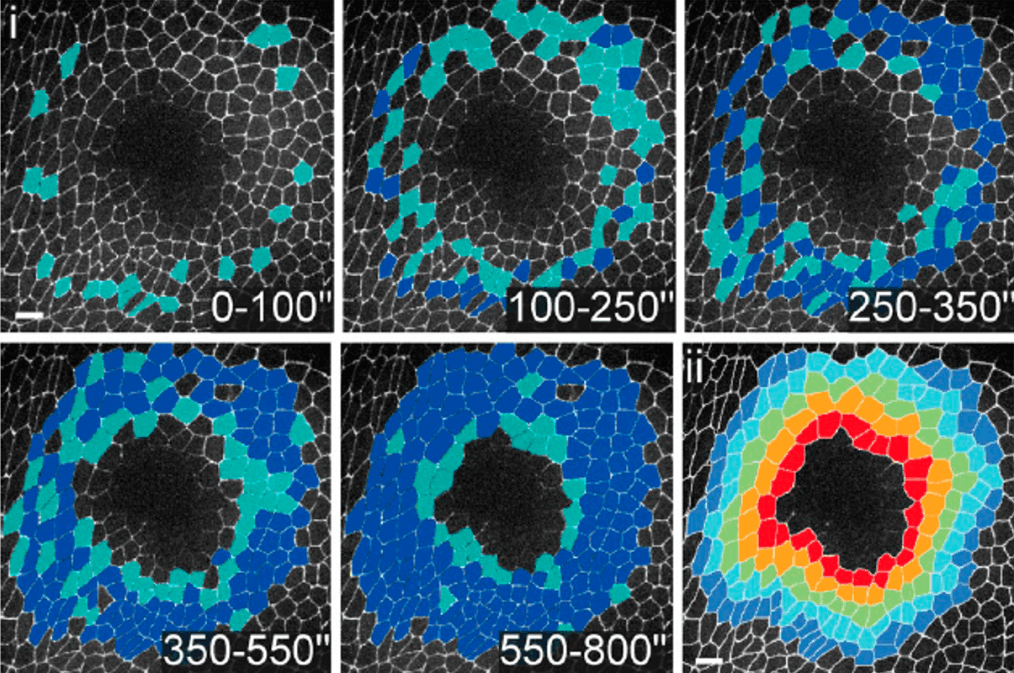
- M. Dureau, A. Alessandri, P. Bagnerini, S. Vincent, Modeling and Identification of Amnioserosa Cell Mechanical Behavior by Using Mass-Spring Lattices, IEEE/ACM Transactions On Computational Biology And Bioinformatics, Vol. 14, n. 6, pp 1476-1481, 2017.

Contacts

Address:

Dime, University of Genoa, via all'Opera Pia 15, 16145 Genova (Italy)
Office: ground floor

Phone:

+39 0103536001

E-mail:

bagnerini at dime.unige.it